728x90
문제 설명
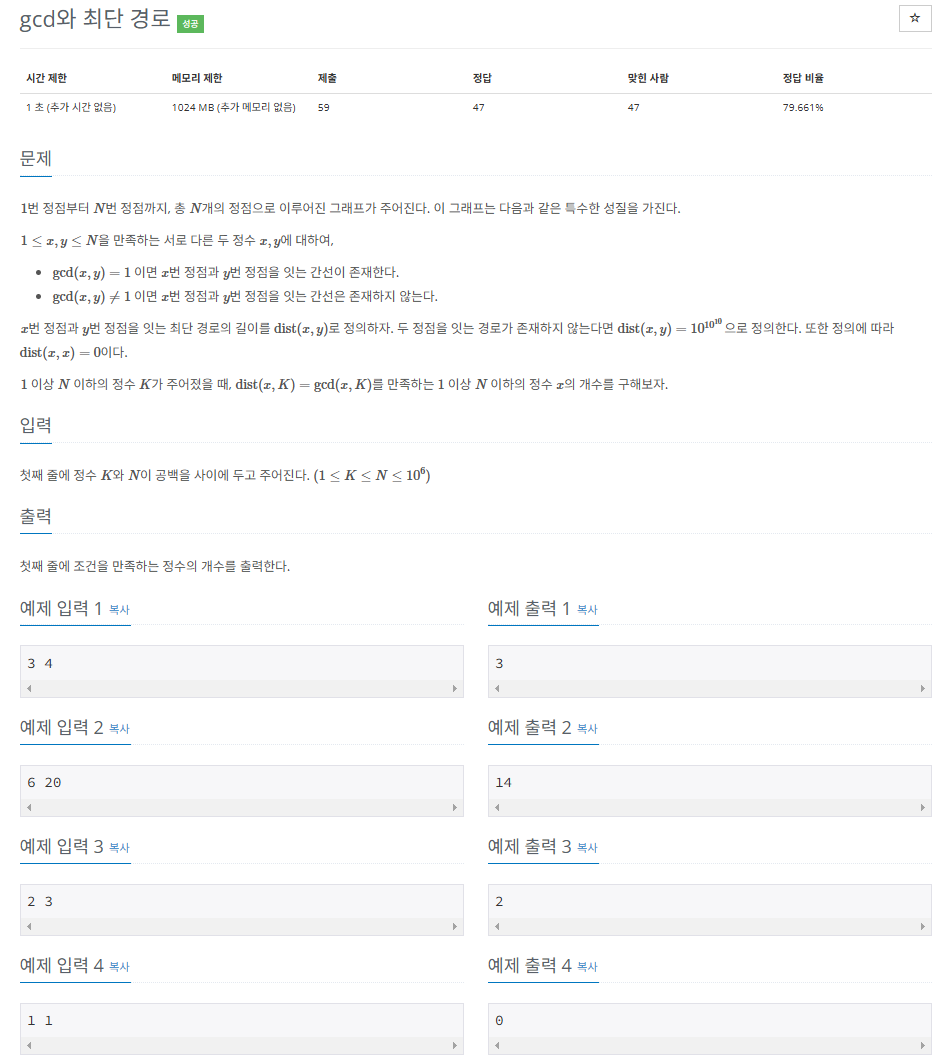
정점이 1번부터 N번까지 있는 그래프가 주어진다. 두 정점 x와 y 사이에 간선이 존재하는 조건은 gcd(x,y)=1일 때이다. 즉, 서로소인 정점들 사이에 간선이 존재한다.
정점 x에서 정점 y까지의 최단 경로 길이 dist(x,y)는 경로에 포함된 간선의 개수로 정의된다. 경로가 존재하지 않으면 dist(x, y) = 10^{10^{10}}으로 정의된다.
정수 K가 주어질 때, 다음 조건을 만족하는 정수 x의 개수를 구해야 한다.
- 1≤x≤N
- dist(x,K)=gcd(x,K)
문제 해결 방법
이 문제는 각 정수 x에 대해 dist(x,K)와 gcd(x,K)를 비교하여 조건을 만족하는 x의 개수를 구하는 문제이다.
그래프의 특성 분석
- 간선의 존재 조건: 두 정점 x와 y 사이에 간선이 존재하려면 gcd(x,y)=1이어야 한다.
- 최단 경로 길이:
- gcd(x,K)=1이면 x와 사이에 직접 간선이 있으므로 dist(x,K)=1이다.
- gcd(x,K)>1이고 x≠K이면, x와 K 사이에 간선이 없지만, 다른 정점을 통해 연결될 수 있다.
- 대부분의 경우 dist(x,K)=2다. 왜냐하면 x와 K 모두 gcd(x,K)의 배수이므로, 서로소인 정점들을 통해 연결될 수 있다.
조건 분석
- dist(x,K)=gcd(x,K)인 경우는 다음과 같다.
- gcd(x,K)=1인 경우: dist(x,K)=1
- K가 짝수이고 gcd(x,K)=2인 경우: dist(x,K)=2
- 특별한 경우 K=1
- 모든 x에 대해 gcd(x,1).
- 그러나 dist(1,1)=0이므로 dist(1,1)≠gcd(1,1)이다.
- 따라서 x=K인 경우는 제외해야 한다.
알고리즘 구현
- 초기화:
- 결과를 저장할 변수 count를 0으로 초기화한다.
- 각 x에 대한 반복:
- x를 1부터 N까지 순회한다.
- x≠K인 경우에만 고려한다.
- gcd(x,K)를 계산한다.
- 다음 조건을 만족하면 count를 증가시킨다.
- gcd(x,K)=1인 경우
- K가 짝수이고 gcd(x,K)=2인 경우
- 결과 출력:
- 최종적으로 count 값을 출력한다.
시간 복잡도 분석
- x를 1부터 N까지 순회하면서 각 gcd(x,K)를 계산하므로, 전체 시간 복잡도는 O(NlogK)이다.
- N≤10^6이고 logK도 크지 않으므로 시간 내에 충분히 계산할 수 있다.
백준 32632 gcd와 최단 경로 문제 파이썬(Python) 정답 코드
import sys
import math
def main():
import sys
input = sys.stdin.readline
K_str, N_str = input().split()
K = int(K_str)
N = int(N_str)
count = 0
for x in range(1, N + 1):
if x != K:
g = math.gcd(x, K)
if g == 1:
count += 1
elif K % 2 == 0 and g == 2:
count += 1
print(count)
if __name__ == "__main__":
main()파이썬 정답 코드 해설
- 입력 처리:
- K와 N을 입력받는다.
- 초기화:
- 결과를 저장할 변수 count를 0으로 초기화한다.
- 반복문:
- x를 1부터 N까지 순회한다.
- x가 K와 같지 않은 경우에만 진행한다.
- gcd(x, K)를 계산한다.
- 조건에 따라 count를 증가시킨다.
- 출력:
- 최종적으로 count를 출력한다.
백준 32632 gcd와 최단 경로 문제 파이썬(Python) 제출 결과

도움이 되셨다면 공감과 댓글 부탁드립니다.
728x90
'Python > 백준' 카테고리의 다른 글
| 백준 아카라카 2 [32652] 파이썬(Python) 코드 + 해설 (0) | 2024.11.14 |
|---|---|
| 백준 GLCCDM [32649] 파이썬(Python) 코드 + 해설 (1) | 2024.11.13 |
| 백준 ABB to BA (Hard) [32293] 파이썬(Python) 코드 + 해설 (0) | 2024.11.11 |
| 백준 토마토 [7576] 파이썬(Python) 코드 + 해설 (1) | 2024.11.10 |
| 백준 KCM Travel [10217] 파이썬(Python) 코드 + 해설 (4) | 2024.11.09 |



